Color Correction — Sensory Intel

Ideally, the expectation is to be able to capture images representing the true colors of the object being imaged. In this effort cameras help by providing White Balance presets [1] [2] that get us there - but only partly!

As some [3] may point out, leaving a camera in Auto WB might not always do the trick. It helps to know the color temperature [4] of the light falling on the object. Being able to measure the color temperature of the lighting source and setting the camera at that WB color temperature carry us forward in our efforts to get to the true colors. It may not be easy to measure color temperature but under controlled environment, e.g. in a studio with custom lighting, it may be possible.

The color temperature is defined by the black body temperature required to radiate light at that hue as shown below [5]. A cheaper way of obtaining the approximate color temperature of a controlled environment is to capture images while varying the color temperature, noting the color error from a standard reference for the greys. The color temperature at which the images transition from a bluish to a reddish hue gives the color temperature that will get images closest to a neutral point with respect to external lighting factors.

Under conditions where finding the exact color temperature of the lighting source is not possible or does not help completely, applying a color correction matrix can prove useful. Details on how to compute a simplified color correction matrix [6] will follow.

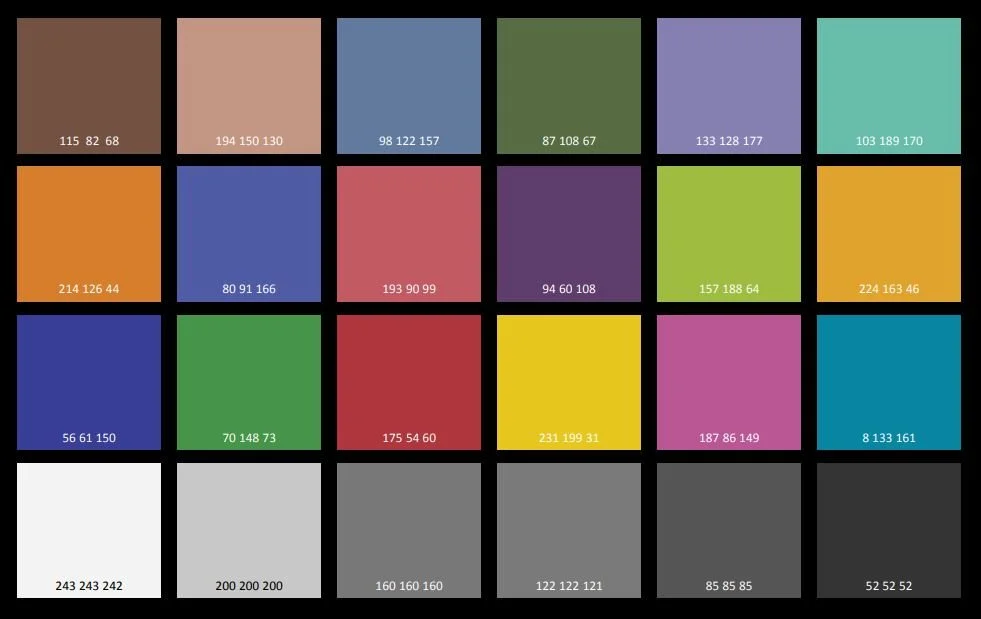
P = Processed camera image R, G, B values on each row. P has 24 rows corresponding to the mean values of each of the 24 color-chart standard colors in the camera image. Size is hence 24 rows x 3 cols.

O = Original reference R, G, B values on each row with 24 rows corresponding to each color-chart reference color value. Size is hence 24 rows x 3 cols.

A = Transformation matrix ( 3 rows x 3 cols OR 4 rows x 3 cols) is the optimal linear transformation matrix that best maps the camera image values of the color samples P into the corresponding reference values of the color samples O.

1 = Column vector of 24 ones can be used in concatenation with P to help compute the offset or shift in brightness level along with the color correction. In this case A is (4 x 3).

Hence each transformed pixel color given by values of O{hat}, is a linear combination of an offset and the camera image values of red, green and blue samples.